What is a Look-up Table?

A Lookup Table, as the name suggests, is an actual table that generates an output based on the inputs. The way that FPGAs are able to do Boolean algebra is by using Look-Up Tables (LUTs).

A LUT, which stands for LookUp Table, in general terms is basically a table that determines what the output is for any given input(s). In the context of combinational logic, it is the truth table. This truth table effectively defines how your combinatorial logic behaves.

In other words, whatever behavior you get by interconnecting any number of gates (like AND, NOR, etc.), without feedback paths (to ensure it is state-less), can be implemented by a LUT.

Here is an example for a lookup table that is implementing the function of an AND gate.

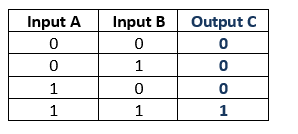
Try now to image that this table is stored in a small RAM.  Inputs A and B are the address pins and C is the data pin.  Every time your address pins are changing they are pointing at a different address entry and they are “reading out” the result which is 0 or 1 based on the inputs.

How to Execute the Boolean Algebra in a Look-up Table

Just like in regular algebra – we can simply a function so that we can reduce the number of gates and lower the cost.

To do this, we use boolean algebra: AB + AC is equivalent to A(B+C).

 

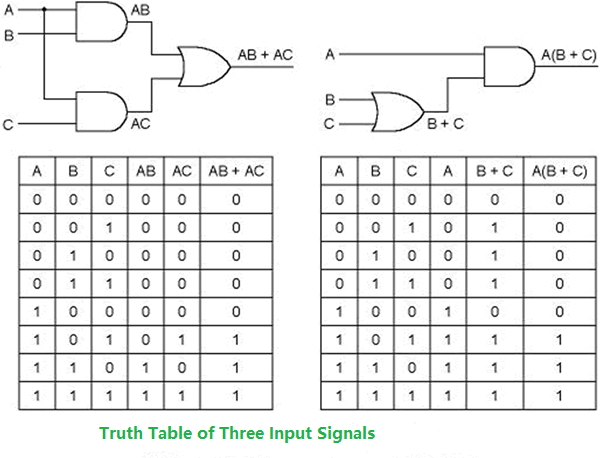
FPGAs use Look-Up Tables or LUTs.  The LUT is programmed by the Digital Designer to perform a Boolean algebra equation like the two that we saw above. As you might expect, all possible combinations of boolean expressions need to be able to be programmed into the Look-Up Table. I will say that again a different way: One 3-Input LUT can make any Boolean algebra equation you can think of using 3 input signals.

LUTs can come in different sizes depending on the FPGA that you are using, but they all behave the same way. 3-Input LUTs were the norm not too long ago, but today 4-Input and even 5-Input LUTs are common. If you need to make a more complicated expression, you can just use more Look-Up Tables. LUTs are one of the two most fundamental components in an FPGA. A single FPGA has thousands of these components. Now that you are more familiar with these wonderfully versatile components, it is time to discuss the other most important element inside of an FPGA

 

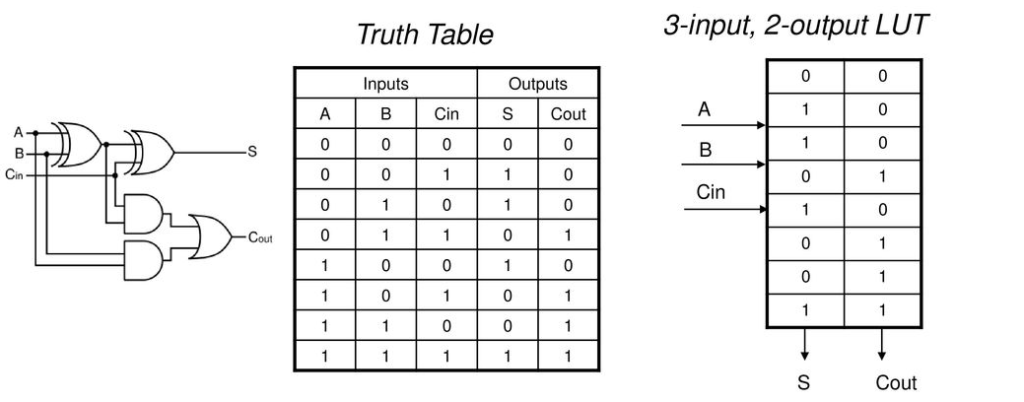
A latch is a circuit that has two stable states which can be used to store one binary digit. Flip-flops and latches are fundamental building blocks used in many sequential circuits and larger storage devices, like shift registers.