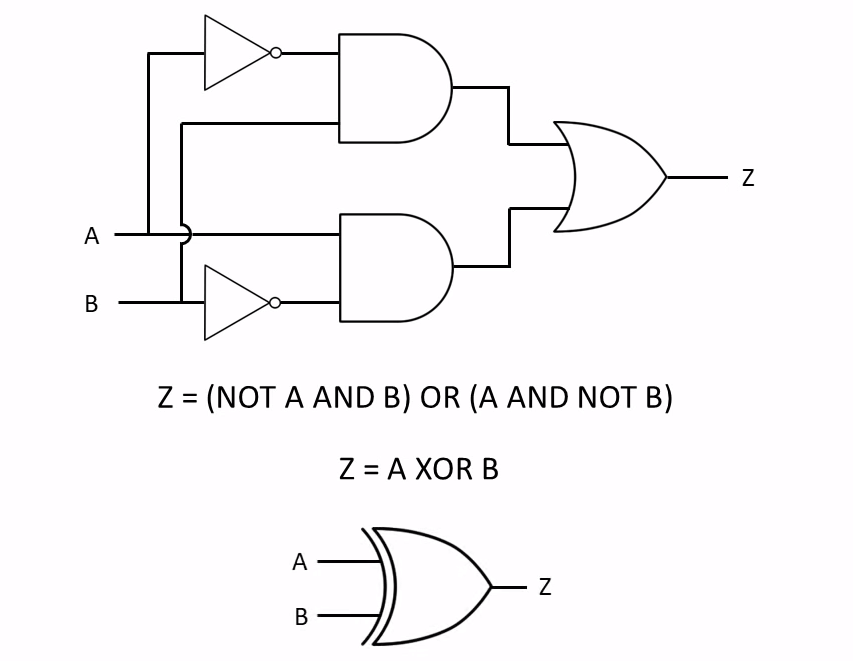
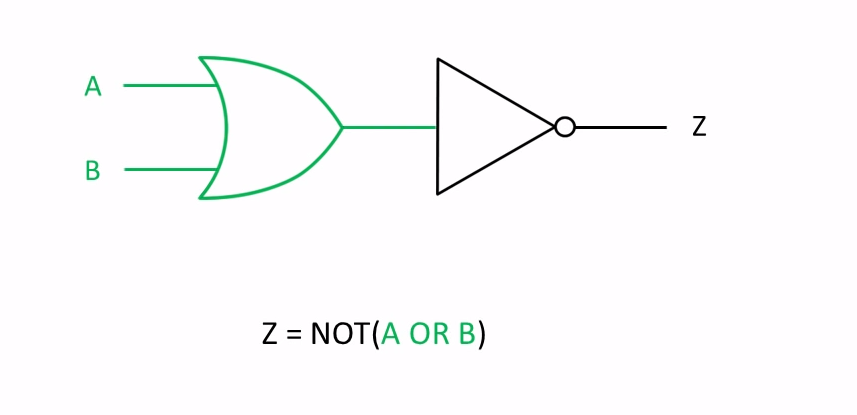
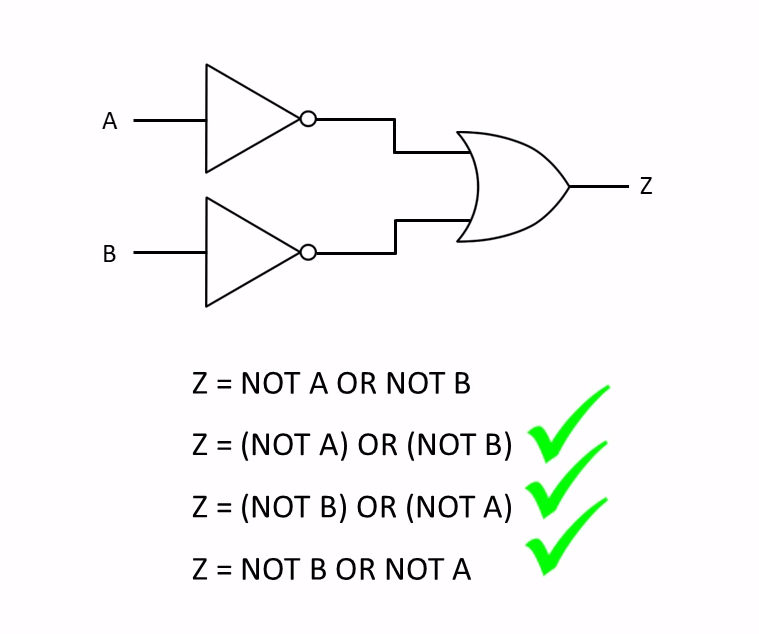
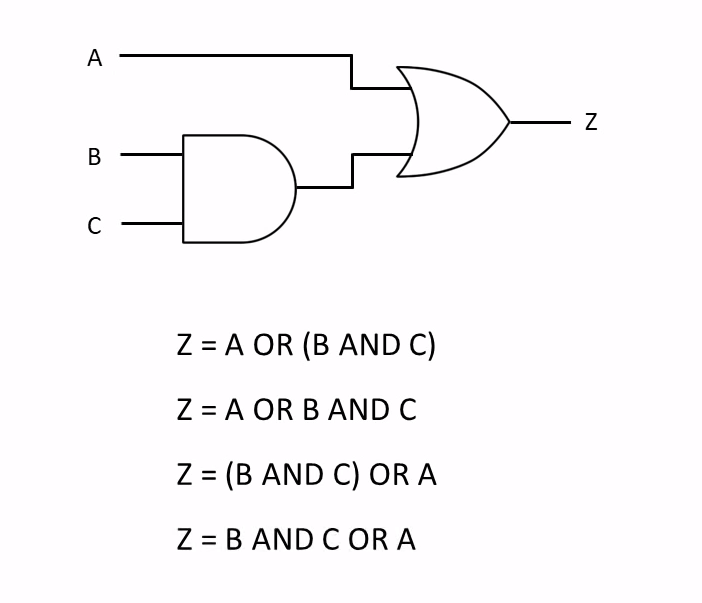
Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854.
Rule in Boolean Algebra
Following are the important rules used in Boolean algebra.
- Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
- Noting of a variable is represented by an ‘ . Thus, Noting of variable B is represented as B’.
- ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
- Logical ANDing of the two or more variable is represented by writing a * between them such as A*B*C.
- XOR ( exclusive or) is represented by “^”
AND gate
An AND gate has 2 inputs and 1 output. Each of these can have the value 0 or 1 and the output value depends on the 2 input values. The output is only 1 when both of the input values are 1. Below is the truth table for an AND gate.
| INPUT | OUTPUT | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
 OR Gate
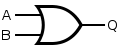
OR Gate
An OR gate has 2 inputs and 1 output. The output is 1 when either of the input values are 1. Below is the truth table for an OR gate.
| INPUT | OUTPUT | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
 NAND Gate
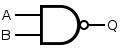
NAND Gate
A NAND gate is an inverted AND gate. It has the following truth table:
| Input A | Input B | Output Q | |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
 NOT Gate
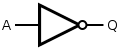
NOT Gate
NOT gate only have one input and one output, the output value is the input reverse value. The output is 0 if the input is 1. The output is 1 if input is 0.
| Truth Table | ||
|---|---|---|
| Input A | Output Q | |
| 0 | 1 | |
| 1 | 0 | |
 XOR Gate
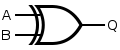
XOR Gate
XOR gate (sometimes EOR, or EXOR and pronounced as Exclusive OR) is a digital logic gate that gives a true (1 or HIGH) output when the number of true inputs is odd. An XOR gate implements an exclusive or; that is, a true output results if one, and only one, of the inputs to the gate is true.
If both inputs are false (0/LOW) or both are true, a false output results. XOR represents the inequality function, i.e., the output is true if the inputs are not alike otherwise the output is false.
A way to remember XOR is “must have one or the other but not both”.
| INPUT | OUTPUT | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
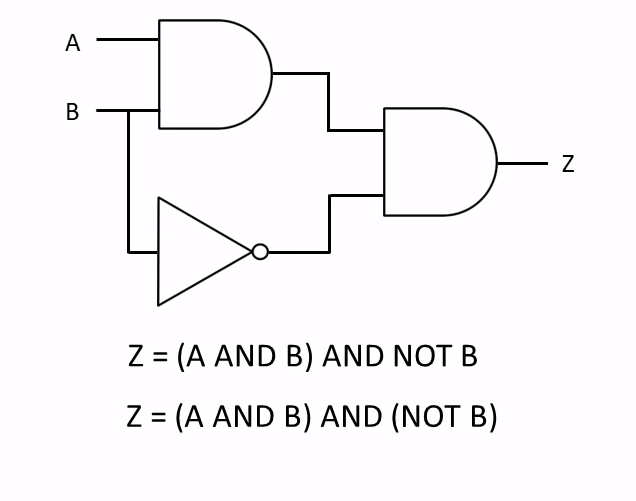
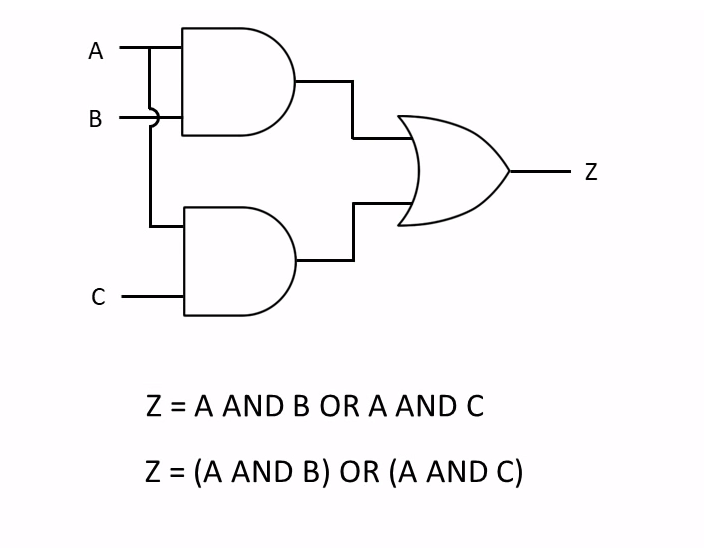
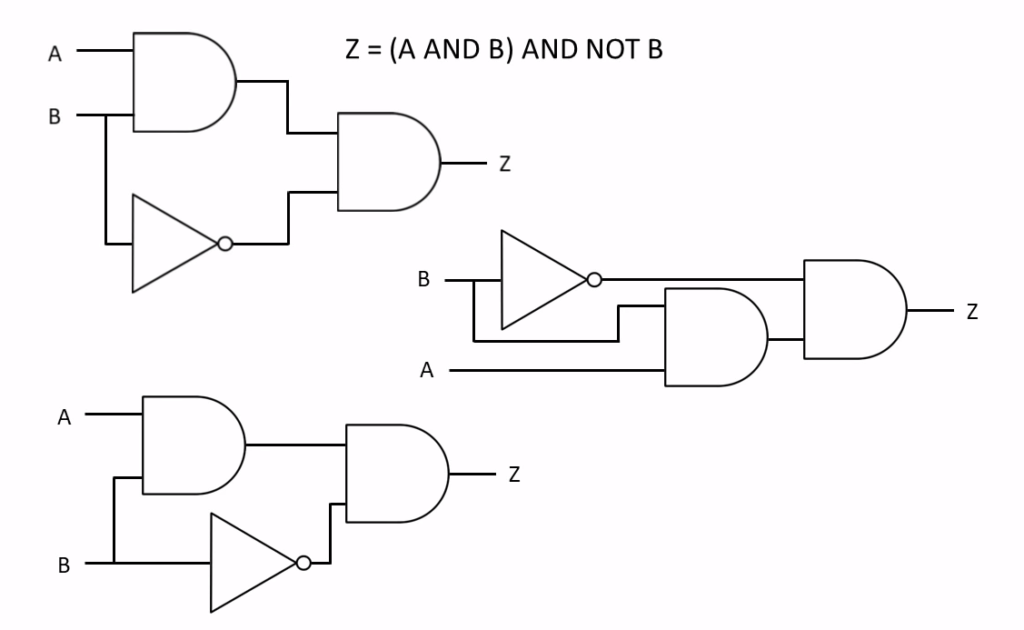
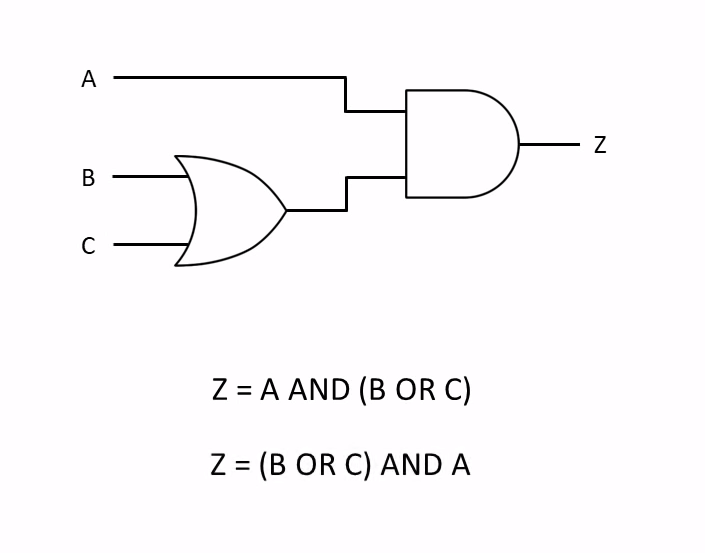
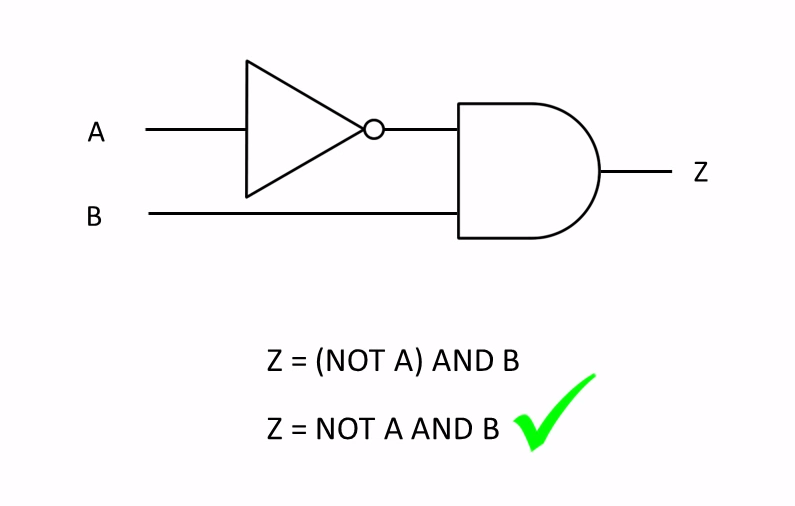
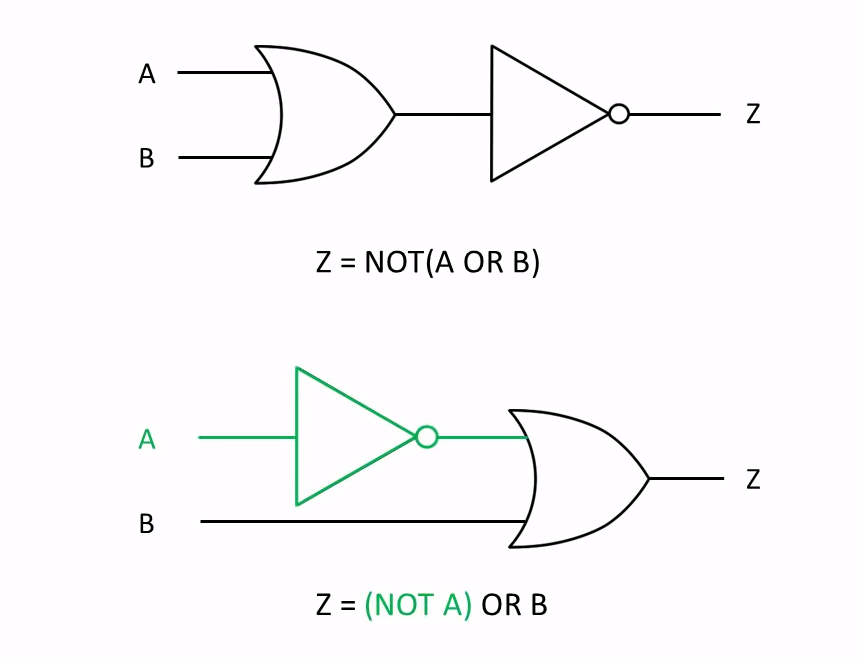
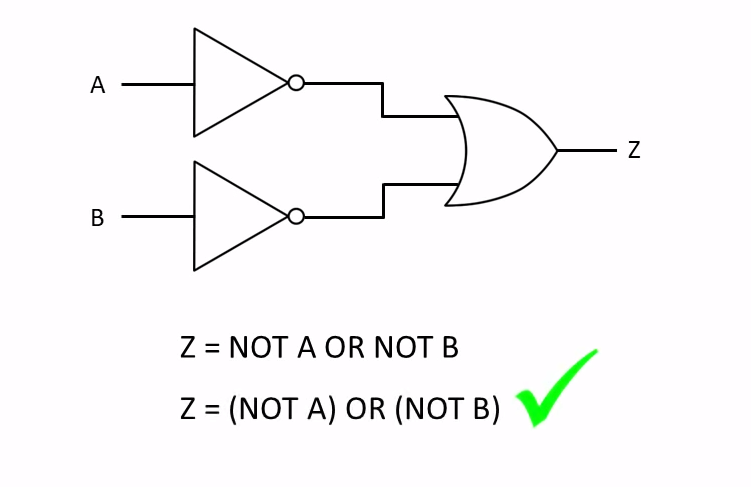
Two or More Logic Gates
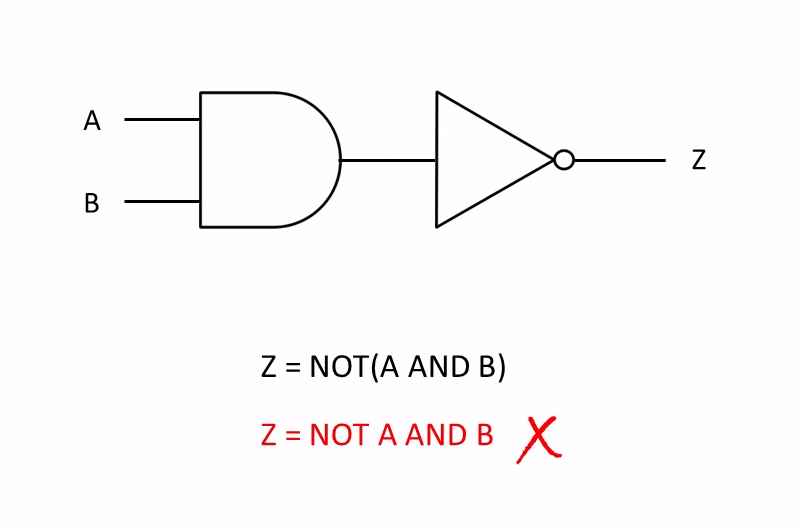
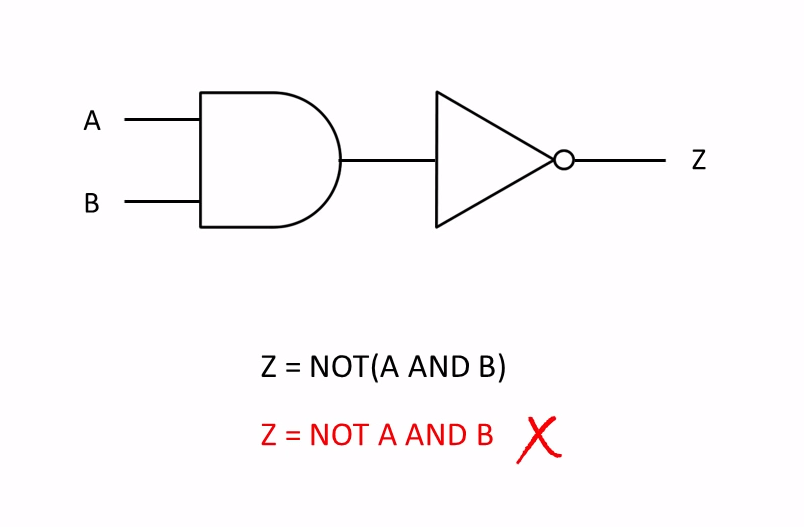
z=NOT (A AND B )