What is Two’s Complement ?

One’s Complement solves the problem of signed bit operations, but there is still a problem that is not solved, that is, now we have two zeros, one +0 and one -0, which are mathematically indistinguishable and take up two codes. To solve this problem, the Two’s Complement was introduced.

The definition of Two’s Complement is that Two’s Complement of a positive number and 0 remains the same, and Two’s Complement of a negative number is the inverse of the corresponding positive number by bit and then +1.

A negative number can also be said to be the One’s Complement +1.

For example:

Also take 8 as an example of a storage unit, Sign-magnitude of -1₁₀ is 10000001 and One’s Complement is 11111110, Two’s Complement is One’s Complement +1, which is 11111111.

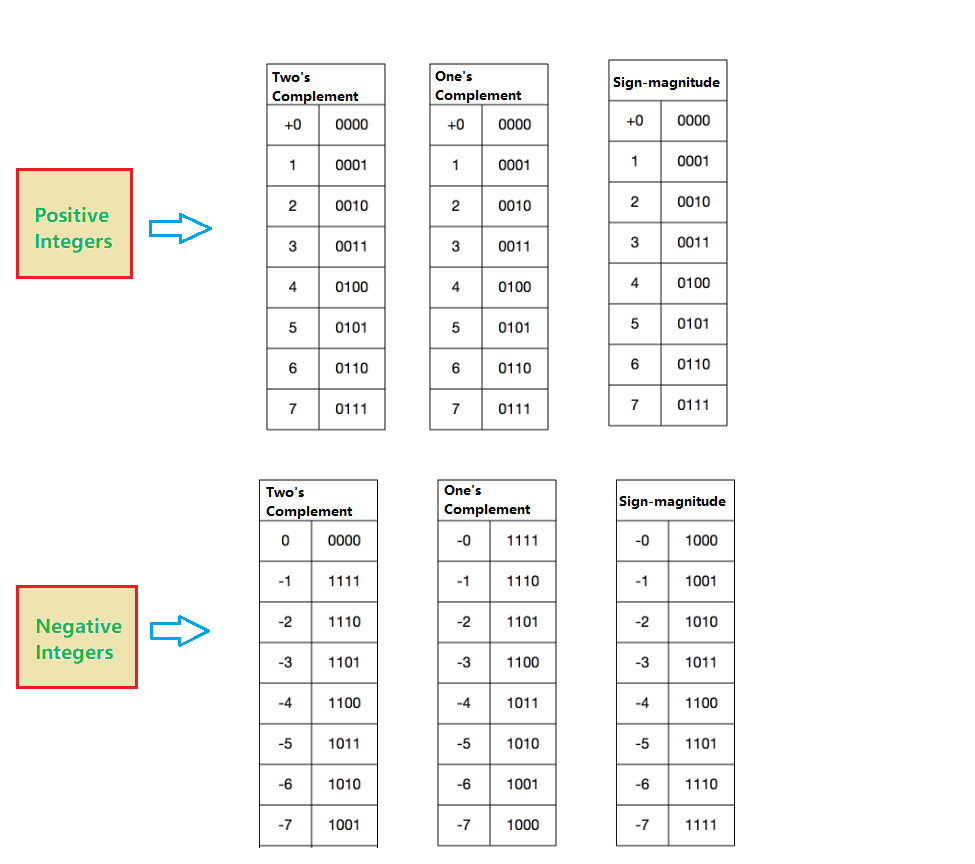
As you can see from above figure, -0 is the same as 0 after taking two’ complement, solving the problem of two zeros.

After -1 to -7, there is an additional code 1000 that can be used to represent -8, which is how we use computers today to store and compute.

2.Why Does Two’s Complement Work ?

In two’s complement figure above,  we can also get -8₁₀ == 1000_2^.  Why ?

2.1 Congruence ( The Same Reminder )

Let us look at the clock below.

The pointer on the dial is pointing to 8. If I want to adjust the pointer to point to 1, what should I do?

1. Turn it clockwise for 5 hours (8 + 5) mod 12 = 1.
2. Turn it counterclockwise for 7 hours (8 - 7) mod 12 = 1.

For a dial, it makes no difference whether we turn it clockwise for 5 hours or counterclockwise for 7 hours. In fact, we can turn it clockwise for 5 + 12n hours or counterclockwise for 7 + 12n hours. From a different perspective, if the pointer is pointing to 8, we cannot tell whether it is 8 o’clock in the morning or 8 o’clock in the evening, based solely on the dial.

From the above phenomenon, we can draw two conclusions:

1. If we regard clockwise rotation as addition and counterclockwise rotation as subtraction, then addition and subtraction in a closed continuous natural number loop can be interchangeable.
2. The effect is the same between 5 and 5 + 12n. That is, as long as the remainder of the two numbers divided by the total number of digits in the loop is the same, the effect is the same.

This law is called congruence in mathematics:

if two integers a and b have the same remainder when divided by an integer m, they are said to be congruent modulo m.

Written as a ≡ b (mod m), a and b are congruent modulo m.

5 mod 12 = 5
17 mod 12 = 5
29 mod 12 = 5

Therefore, 5, 17, and 29 are congruent modulo 12.

2.2 More About Congruence

In order to understand why computers use two’s complement, we need to know that, due to the limited memory length of computers, computer operations are essentially modular arithmetic.

For example, with a 32-bit integer length, a computer can represent 2³² or 4,294,967,296 different states. When we calculate 1 + 2 on a computer, it is essentially a modular arithmetic operation.

a ≡ 1 (mod 4294967296)
b ≡ 2 (mod 4294967296)
r ≡ a + b ≡ 3 (mod 4294967296)

Returning to the example of the clock face, let’s write 12 on the clock face as 0. Now our clock face represents 12 numbers from 0 to 11. We take 0 as the starting point and use 12 as the modulus. Turning the clock hand counterclockwise gives us negative numbers, while turning it clockwise gives us positive numbers. For example, if we turn the hand counterclockwise by one position, we get -1. Since -1 and 11 are congruent modulo 12, they are equivalent. By using this property of congruence, we can introduce negative numbers.

Now, let’s consider putting the numbers 0000 0000 to 1111 1111 on a clock face. The pattern is the same as that of the clock face with only 12 positions. For example, 11111111 can represent 255 or -1, and in modular arithmetic, they are equivalent. With 8 bits, we have a total of 256 states. Since we want to introduce negative numbers, we want the same number of positive and negative numbers.

Therefore, we represent 1 to 127 as 0000 0001 to 0111 1111, and -1 to -127 as 11111111 to 10000001, with two additional numbers 0000 0000 and 1000 0000. Naturally, 0000 0000 represents 0. What about 1000 0000? It can represent either 128 or -128, but for consistency and ease of data processing, we use it to represent -128, so that the highest bit of all negative numbers is 1. The binary codes for these negative numbers are called two’s complement.

After all the introduction, let me tell you where -8 came from. It seems like we have deviated from the concept of two’s complement. What is the essence of two’s complement? In fact, two’s complement is just a mathematical rule behind the previous content. We use 1111 1111 to 1000 0000 to represent -1 to -128.

3. How are Integers Stored in Memory ?

Using two’s complement representation, we can handle both positive and negative numbers with a single format.

This simplifies arithmetic operations because addition and subtraction of two’s complement numbers are done in the same way as for unsigned numbers, using only the regular binary addition algorithm.

In addition, converting between two’s complement and unsigned representation can be done with a simple bitwise complement operation, which does not require any additional hardware.

Therefore, using two’s complement representation for storing and processing numbers in computer systems is a very efficient and practical approach.