One’s Complement

From the binary of the true value to sign-magnitude, we took a step forward and introduced negative numbers in the computer.

But there is a serious problem with sign-magnitude:

-1₁₀ is binary 10000001₂
1₁₀ is binary 00000001₂

As you know,

1 + 1 = 2

But 1000 0001 + 0000 0001 = 1000 0010

According to the rules of sign-magnitude, 1000 0010₂ == 2 ₁₀

This obviously does not work, and the circuit cannot be designed. For humans, it is easy to tell if the first digit is a sign bit, and we choose whether to add or subtract the absolute value of the subsequent digit and get at a result based on the sign.

But for a computer it is very complicated to separate the sign bit, and if we make the circuits for basic addition, subtraction, multiplication and division operations very complicated, then the performance of the computer is obviously very poor.

Now the problem is how to make the sign bit can participate in the operation and form a perfect logic.

To solve this problem, we introduced One’s Complement, which is defined as:

If the number is positive, it remains unchanged,
If the number is negative, it is inverted by bit except for the sign bit.

See the following figure for details.

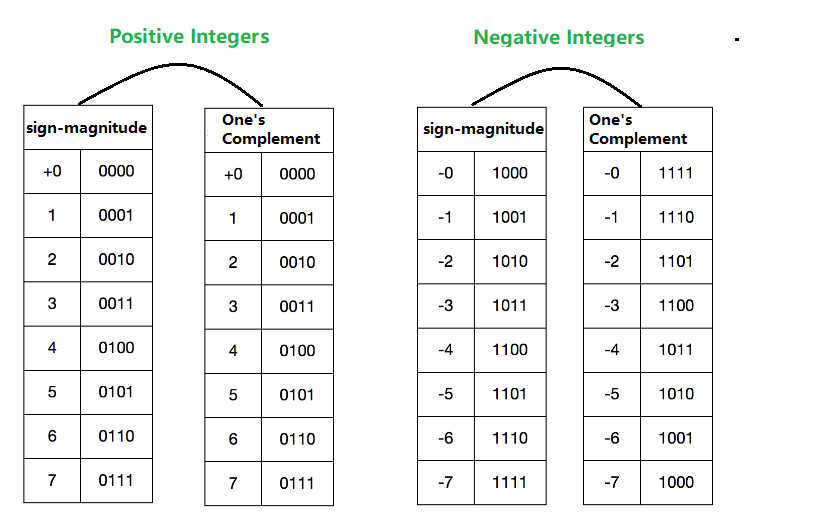
Through the design logic of One’s Complement, we can find that the positive and negative numbers are now added to obtain 1111, which is -0. Now we have the ability to design the circuits and then use the computer to store and calculate.