Sign-magnitude is a binary fixed-point representation method for numbers in computers.
To perform calculations, computers must store numerical values. The simplest way is to use machine code as our true value. For example, an 8-bit storage unit can store 256 different numbers from 00000000 to 11111111, representing true values from 0 to 255.
However, this design is not meaningful because we need to calculate negative numbers. To introduce negative numbers, the Sign-magnitude was designed: using the first bit of the storage unit to represent the sign, 1 for negative and 0 for positive, and the remaining bits to represent the absolute value of the true value. Similarly, using an 8-bit storage unit as an example, we can still represent 256 numbers using the Sign-magnitude method, ranging from 11111111 to 01111111, with a true value range of -127 to 127.
You may notice that there are only 255 possible true values, because both 10000000 and 00000000 represent 0.
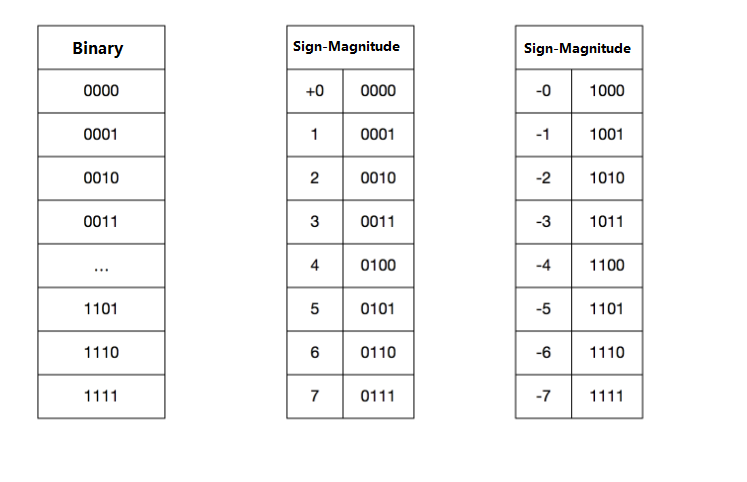
From the binary of the true value to the sign-magnitude, we can see that there is no difference for the machine. It is just that we give the same binary number different meanings through mathematical methods, so that the computer can meet our calculation needs. Following this idea, we can also understand the one’s complement and the two’s complement.